Neural Networks and Deep learning: An Overview

Neural networks and deep learning are two of the most important concepts in the domain of Machine Learning. Innovative applications like cancer detection, image recognition, speech recognition, machine translation, driverless cars, intelligent personal/home assistants etc., all have been made possible by utilizing deep learning knowledge.

At the heart of neural networks and deep learning, a lot of complex linear algebra and mathematics is involved. The aim of this blog, however, is not to explore the mathematical features of a neural network but to explain the concept of neural networks and deep learning in an easier way.

Introduction to Neuron

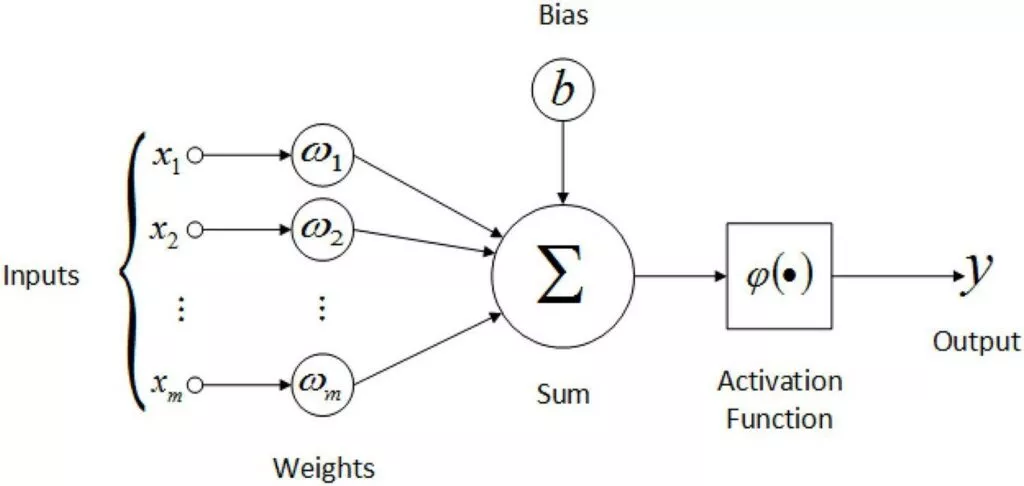
There is an important object in any neural network called “Neuron”.  Let’s see how an individual artificial neuron works:

– Every neuron has inputs (x) which are the processed outputs of the preceding neurons.
– Weight (w) is then associated with each input (x), their products are then added together to form an expression similar to the one given below:
x1*w1 + x2*w2+ x3*w3 + … + xn*wn
– A bias ‘b’ is added to the above expression and passed through an activation function, the result of which is the value of the given neuron.

Consider the following diagram to better understand the points above:

Bias

A bias is an extra input to the neuron. It makes sure that even if the weighted sum of inputs to a neuron is zero, there is some value for neuron activation.

Activation function

Activation functions are used to add non-linearity to neural networks. They squeeze the values into a smaller range. There are different activation functions available that are used in deep learning. For example, a binary step function squashes the value to 0 or 1. It takes the input and if the input is less than 0, the output is 0 and if the input is equal or greater than zero, the output is 1.

You can read more about different types of activation functions and their details in this blog:

https://missinglink.ai/guides/neural-network-concepts/7-types-neural-network-activation-functions-right/

A single neuron can be used to solve a relatively simpler problem but to solve complex real-world problems, we need more neurons and that’s where deep learning comes into picture.

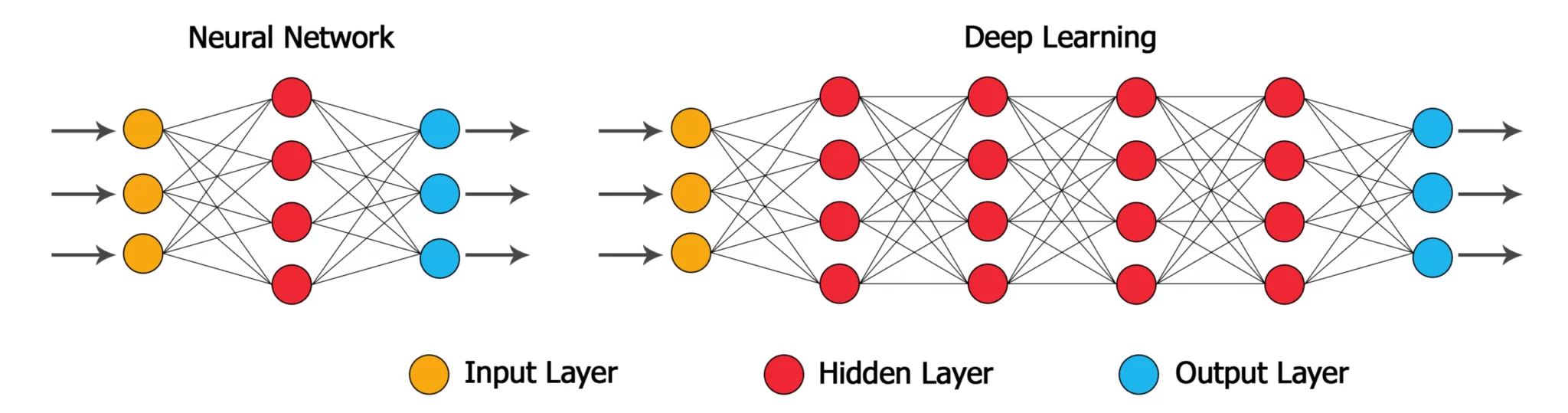
Neural Network vs Deep neural network

The following diagram depicts the difference between a neural network and a deep neural network.

All these individual nodes are neurons, they have the same structures and are working as explained above. Neurons are categorized into different layers:

• Input layers feed the input,
• neurons in the hidden layers do the processing, and
• the output layer gives output.

If there are one or two hidden layers in the network, then it is classified as a neural network. If there are more than 3 hidden layers in a network, then it would be categorized as a deep neural network.

Note: The working of each neuron in a complex neural network remains the same. However, different neurons may have different activation functions.

Forward and backward propagation

At the start of the model training, the parameters (weights and bias) are initialized randomly. The goal of the model training is to come up with the most suitable value of each parameter per neuron to minimize the error quotient of the model under training.

Forward Propagation:

The following information flow from the input to the output layer is called ‘forward propagation’:

• The input from the input layers goes to the first hidden layer,
• Each neuron in that hidden layer calculates the output and passes it to the next layer. The output from this layer becomes the input to the next layer and each neuron in the second hidden layer calculates the output and pass it to the next layer. This process goes on till the output layer is reached.
• The output layer produces the final output of the network. We compare this output with the known output(actual) and calculate the error. Error is the difference between the actual output and the output produced by the neural network. There are different types of error calculating algorithms like mean squared error, root mean squared error, cross entropy and many more. These are also known as cost functions and can be used depending upon the problem that you are trying to solve.

Backward Propagation:

The following (reverse) information flow from the output into the hidden layer on to the input layer is known as ‘backward propagation’:

• After calculating the error (derived from the result of ‘forward propagation’), we move back in the reverse direction from output layer to the hidden layer.
• The error of each neuron and update on the weights and bias (hyper parameters) is calculated accordingly.
• An optimization algorithm is used to update these parameters. Gradient descent is an example of such optimization algorithms.

Both forward and backward propagation are performed (multiple times over) to train the neural network. After training, we test our model for performance. If the desired performance is achieved, we deploy our model in production to make predictions on real-world data. Otherwise, we can perform further iterations with different values for model parameters to improve model performance. Different model parameters include optimization algorithms, activation functions, the number of hidden layers, and the number of neurons in a hidden layer.

In my upcoming blogs, I will be explaining the different types of neural networks such as CNN’s, RNN’s and their applications. I will also be going through “Transfer learning” which makes training neural networks easier by utilizing the model’s previous learning to perform a different task.

If you have any questions on Neural Networks and Deep Learning, don’t hesitate to reach out! Comment below!